直接当ページへの来訪者は
直接当ページへの来訪者は| 『水底にある物体に浮力は働くか?』の実験結果へ |
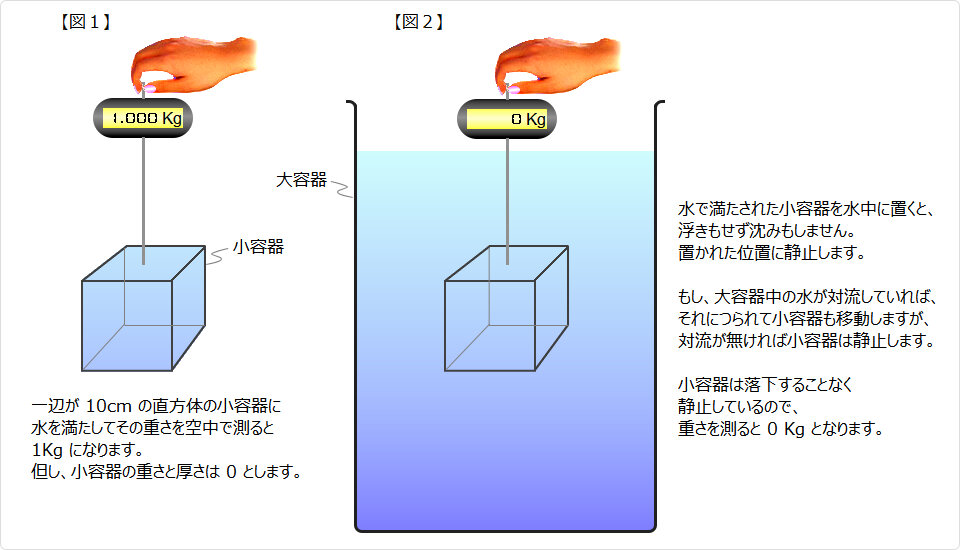
 アルキメデスの原理:浮力の正体の一考察 アルキメデスの原理:浮力の正体の一考察先ず、現実の理解を深めます 水中にある硬い小容器中の水の重さ測ってみます |
||||||
 |
||||||
 |
||||||
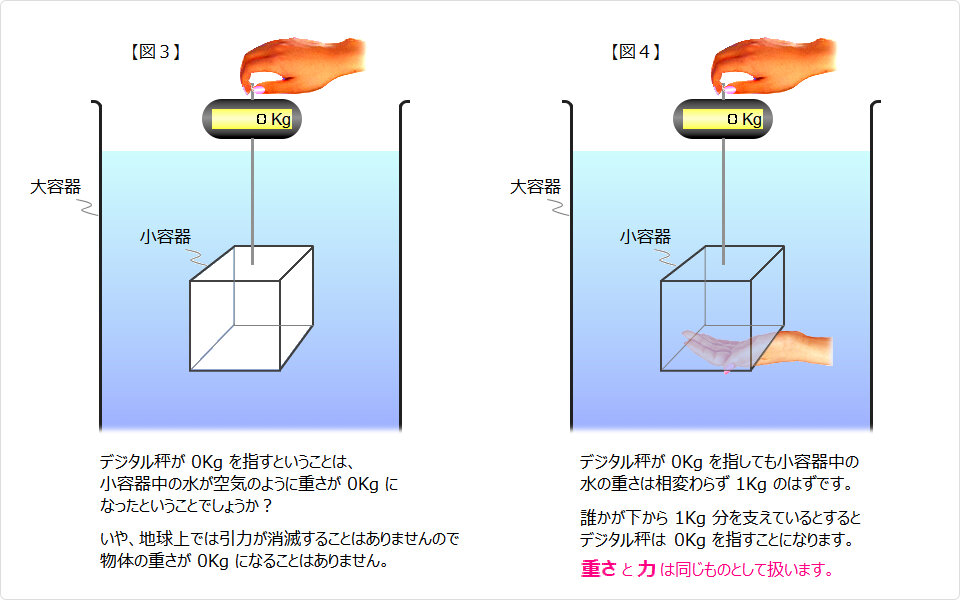
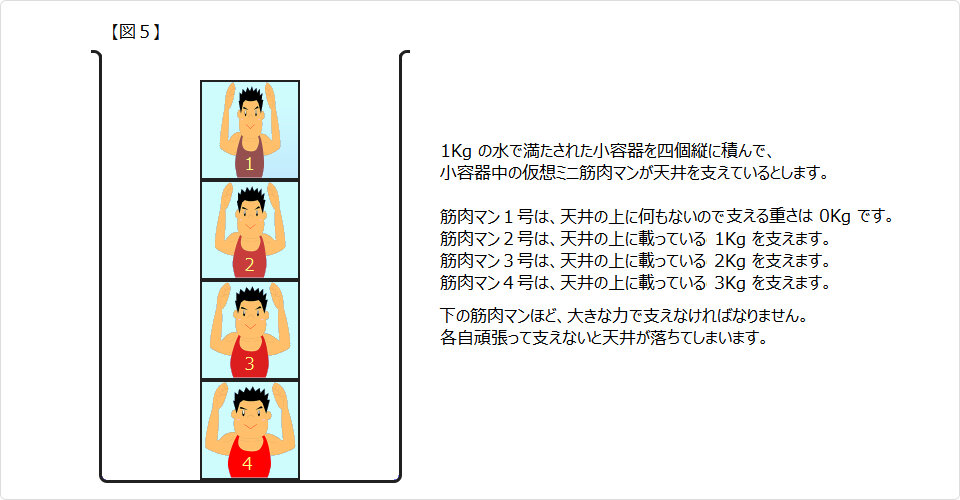
 では、いったい誰が小容器を支えているのでしょうか では、いったい誰が小容器を支えているのでしょうか |
||||||
 |
||||||
 |
||||||
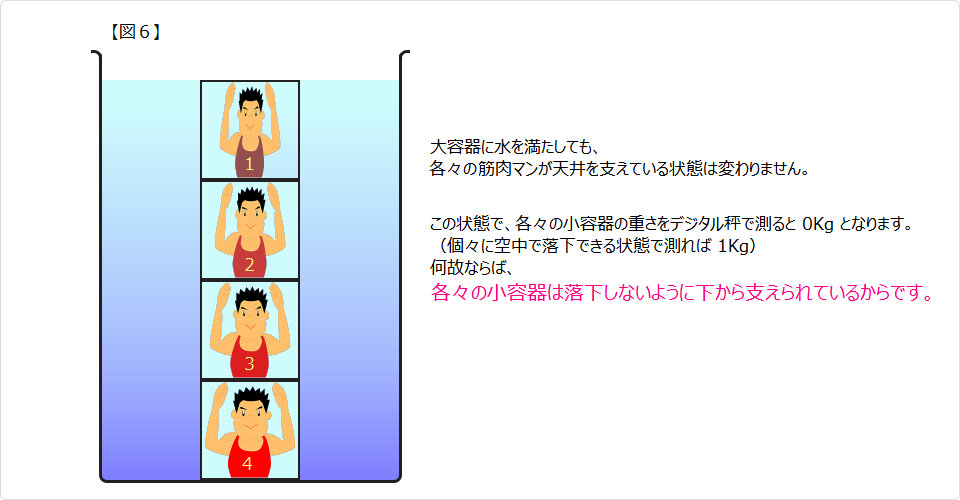
| ▲ 実際には、筋肉マンではなく硬い容器で支えています。 |
||||||
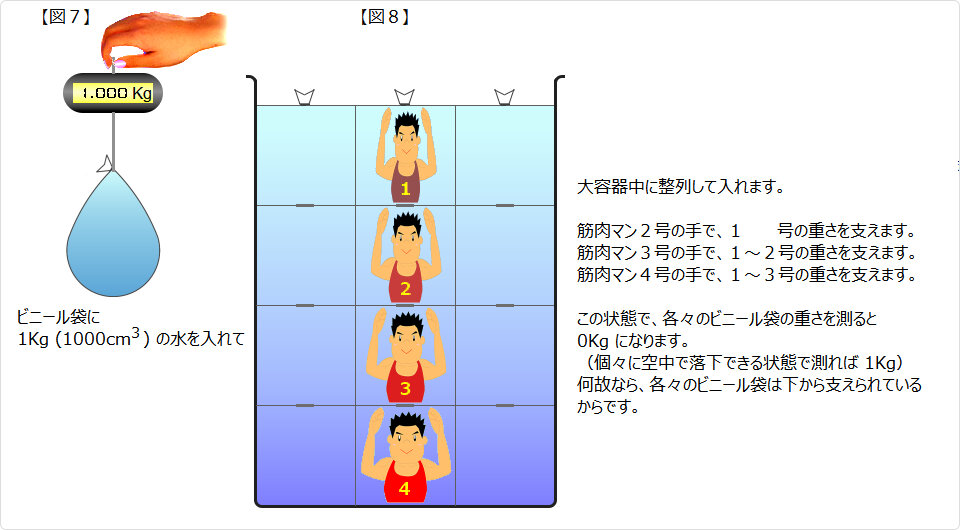
 次に、柔らかい容器に入った水で考えてみます 次に、柔らかい容器に入った水で考えてみます |
||||||
 |
||||||
| ▲ 実際には、筋肉マンではなく 硬い容器の場合は、硬い容器が支えていましたが、 柔い容器の場合は、容器中の水で支えています。 |
||||||
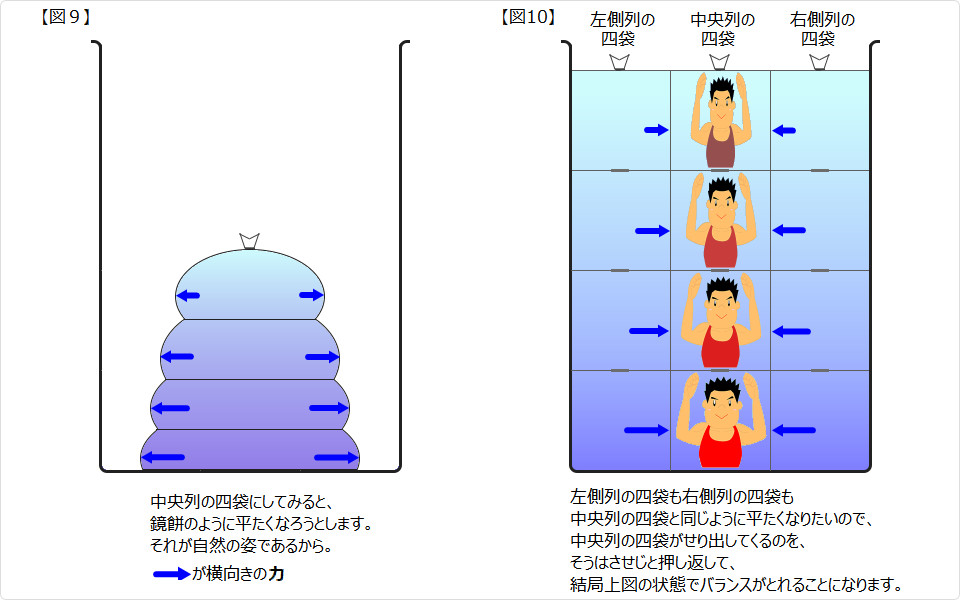
 水の重さによって、横向きの力が発生する仕組み 水の重さによって、横向きの力が発生する仕組み(概念図) |
||||||
 |
||||||
| ■ 以下 cgs 単位系 で話を進めます。 |
||||||
 水の重さによって、水圧が発生する仕組み 水の重さによって、水圧が発生する仕組み(いよいよ水圧という言葉がでてきます) |
||||||
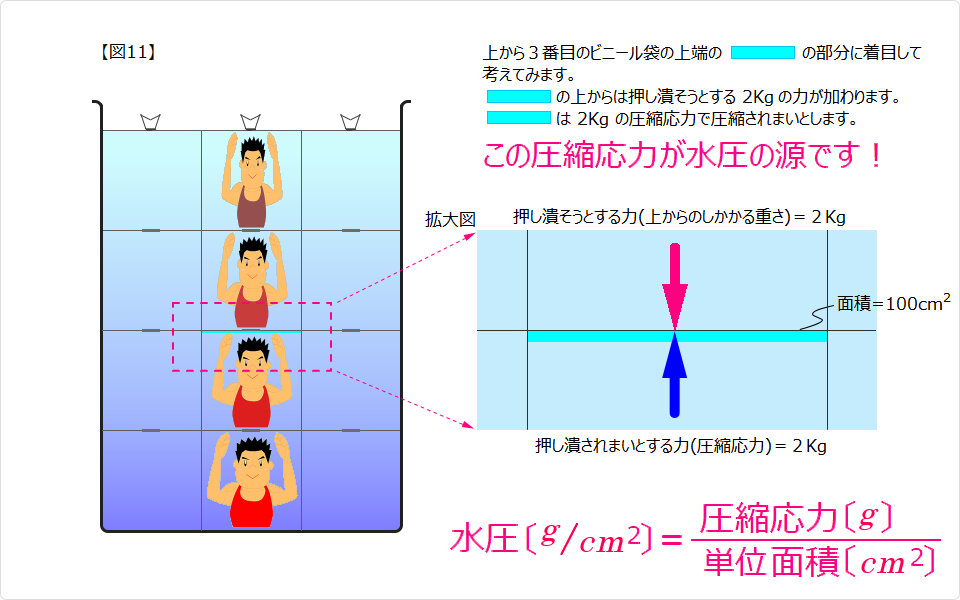 |
||||||
| ▲ 圧縮応力(のしかかる重さと同じ)は、 圧縮応力 F [g] = 面積S [cm2]×水深H [cm]×水の密度ρ[g/cm3] となります。・・・・・・・・・・・(式1) ■ 水圧は水の圧縮応力が源です。 水圧とは、かかる圧力の全部ではなく単位面積たとえば1cm2 あたりにかかる圧力です。 1cm2 あたりにかかる水圧は、 水圧P [g/cm2] = 圧縮応力F [g] / 単位面積[cm2] 水圧P [g/cm2] = 面積S [cm2]×水深H [cm]×水の密度ρ[g/cm3] / 単位面積[cm2] となります。 ・・(式2) ■ 実際、液体でも圧力をかけると極々微量の体積変化をします。 気体では分子間距離が大きいので容易に体積変化しますが、 液体では分子間距離が小さいので分子間斥力が大きく働き、体積変化は極々微量にとどまります。 ※ ここでは 力の単位を g で表していますが、一般には N で表します。 ※ 実際には大気圧がかかりますが、ここでは触れないでおきます。 |
||||||
 水圧はあらゆる方向に作用します 水圧はあらゆる方向に作用します |
||||||
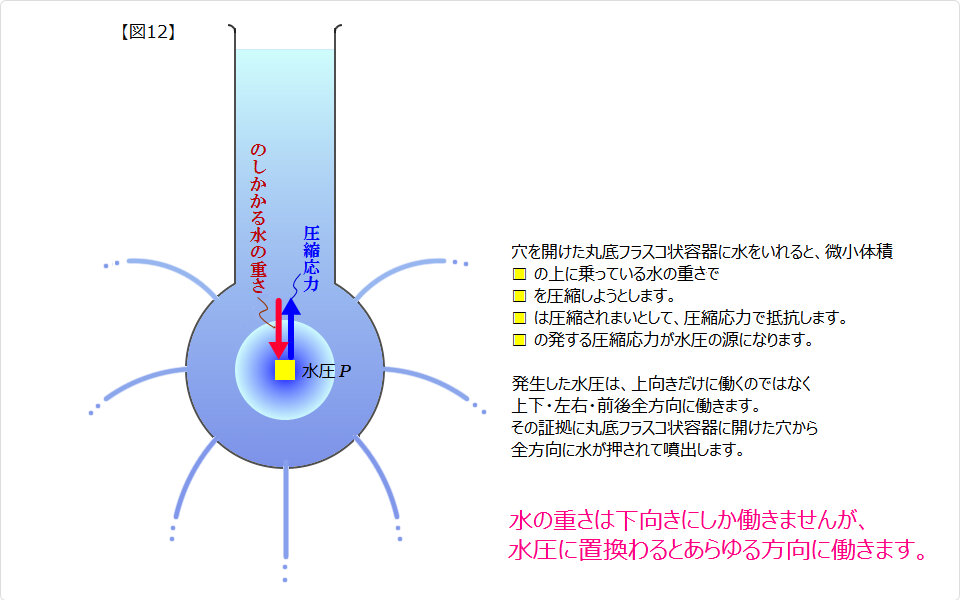 |
||||||
| ▲ 水圧が四方八方に作用するのは『エネルギー等分配の法則』に因ります。 ■ ブラウン運動に因るというもっともらしい説もありますが、 そもそもブラウン運動とは、花粉から漏れ出した微粒子が不規則に運動する現象に付けられた呼称であり、 水分子そのものがブラウン運動するのではありません。 Wikipedia の http://ja.wikipedia.org/wiki/%E3%83%96%E3%83%A9%E3%82%A6%E3%83%B3%E9%81%8B%E5%8B%95 ■ 水圧はあらゆる方向に作用する、ということは、 ↓ 特定の方向を持たないことと同じ、ということは、 ↓ 水圧は方向を持たないスカラー量と等価です。  |
||||||
 |
||||||
 水圧による力は面に垂直に作用します 水圧による力は面に垂直に作用します |
||||||
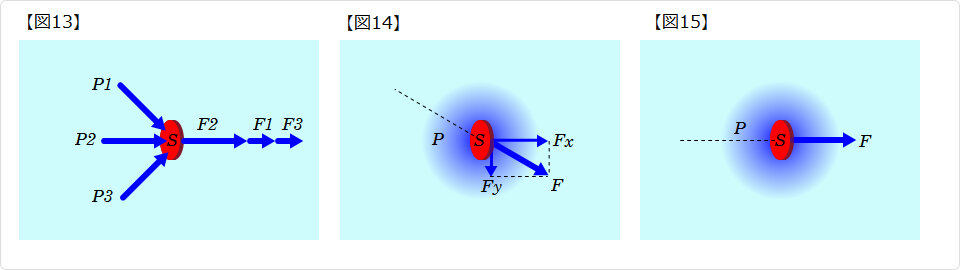 |
||||||
| ▲ 水中の面 S にかかる水圧による力は パスカルの原理:作用面に垂直性 に因り 面 S の法線(面に直角)の向きになります。 ■ 図13 は もっともらしい説で、 水圧はあらゆる方向に働くので、面 S はあらゆる方向から水圧がかかることになります。 上側からの水圧 P1 と 下側からの水圧 P3 により、上下方向の力は相殺されるので、 結局合力は右方向を向くと言う説です。 しかしながらこの説では、水圧 P2 による 力F2 に、 水圧 P1 と水圧 P3 による力の水平成分 F1 と F3 が加算されてしまうことになり、これは不合理です。 水圧 P2 による力は F2 だけで充分です。 ■ 図14 は 面 S の表面に沿う力(せん断力)Fy を起こしてしまうので、静止流体中では不合理です。 面に斜めの力がかかると、せん断力により円盤は移動または回転してしまいます。 密度 ρ=1 の円盤ならば静止するはずです。 ■ 結局 図15 のように 面 S にかかる水圧による 力F は、面 S の法線(面に直角)の向きになります。 ■ 静止流体中では接線応力は働かないという理論は 同志社大 エネルギー機械工学課 水島研究室 の 流れ学・流体力学サブメニュー で開くページで、 流れ学 >ダウンロード 流れ学 I で開く |
||||||
 水圧だけでは力になりません 水圧だけでは力になりません水圧が面に働くと はじめて方向を持った力になります |
||||||
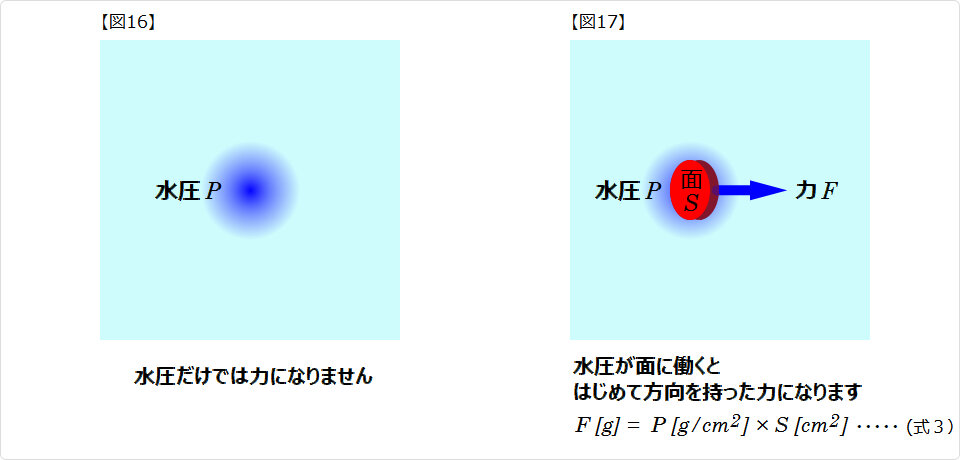 |
||||||
| ▲ 力が発生する理由として、 『面で水分子が跳ね返る際に、運動量変化に等しい力積 Ft = 2mv を面にかける』という説がありますが、 これは気体ではよく知られたことですが、液体にもあてはまるのでしょうか? 水深によって水圧による力が増えるのは、 水分子の質量 m が増えた結果なのか? 水分子の速度 v が速くなった結果なのか? 水分子の数が増えた結果なのか? 衝突の回数が増えた結果なのか? 釈然としません。 |
||||||
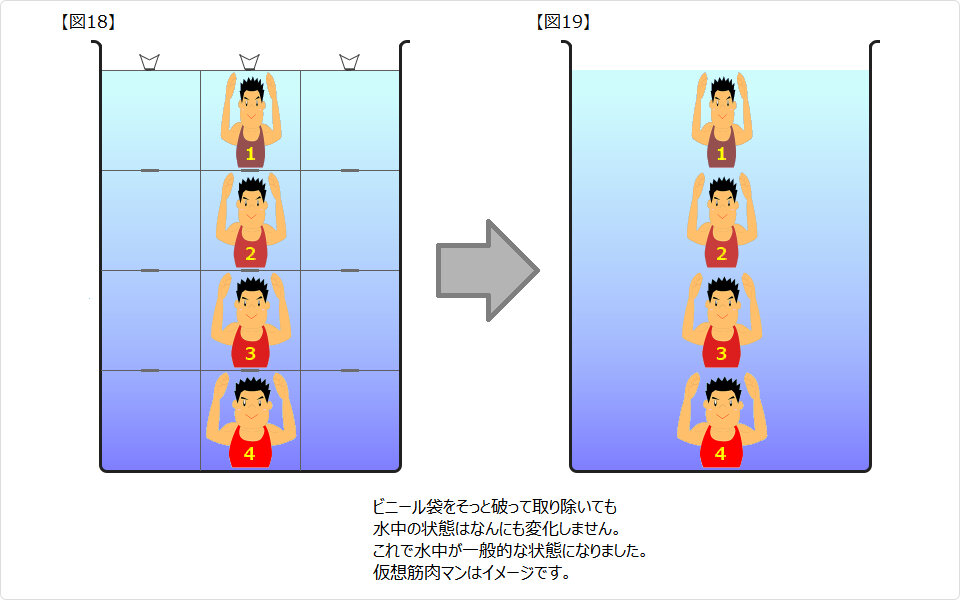
 ビニール袋の呪縛から開放します ビニール袋の呪縛から開放します |
||||||
 |
||||||
| ここまでのまとめ。 ★ 水圧は圧縮応力が源。 ★ 水圧はあらゆる方向に作用し、方向を持たないスカラー量と等価です。 ★ 水圧が面に働くと、はじめて方向を持った力になります。 ★ 水圧による力は面に垂直に作用します。 |
||||||
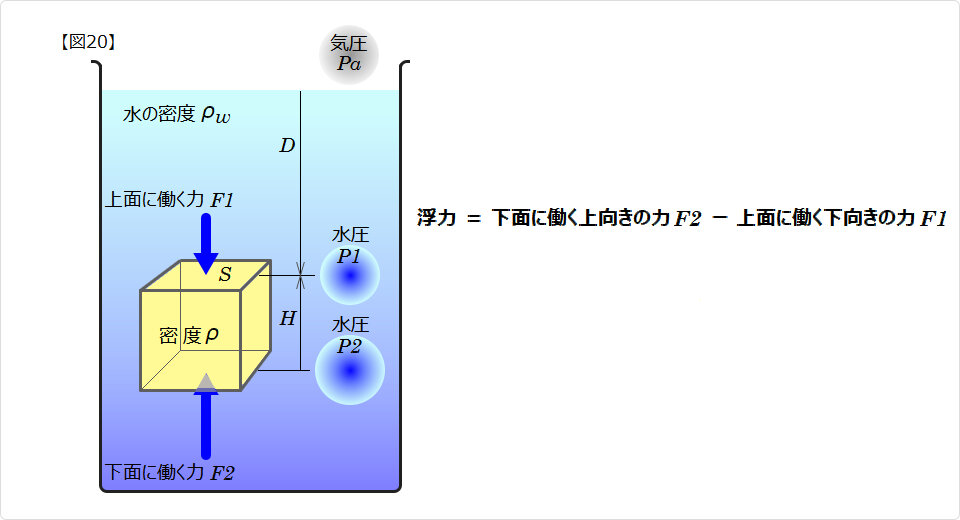
 いよいよ浮力の説明に入ります いよいよ浮力の説明に入ります |
||||||
 |
||||||
| ▲ 上面積S [cm2] 高さH [cm] の立方体に働く浮力を計算してみます。 ここまでは、大気圧は無視して来ましたが、ここでは気圧も含めて考えることにします。 〔1〕先ず、水圧 P1 と P2 を算出します。 水圧 P1 [g/cm2] = 水深 D [cm] × 水の密度ρw [g/cm3] + 気圧 Pa [g/cm2] 水圧 P2 [g/cm2] = (水深 D [cm] + 物体の高さ H [cm]) × 水の密度ρw [g/cm3] + 気圧 Pa [g/cm2] 〔2〕物体の上面と下面に働く力を算出します。 物体の上面に働く力 F1 [g] = 水圧 P1 [g/cm2] × 面積 S [cm2] 物体の下面に働く力 F2 [g] = 水圧 P2 [g/cm2] × 面積 S [cm2] 〔3〕物体の上面と下面に働く力の差を算出します。これが浮力となります。 F2 − F1 [g] = 面積 S [cm2] × 物体の高さ H [cm] × 水の密度ρw [g/cm3] ・・・・・・・・(式4) 式4から次のことが導かれます 浮力は物体の水中の体積の水の重さに等しい 浮力は物体の密度に依存しない 浮力は水深に依存しない 浮力は気圧に依存しない 〔※〕立方体の側面にかかる水圧による力は、お互いに大きさが等しく逆向きなので相殺されて 0 になり、 立方体は水平方向へは移動しません。 ■ 物体の重さ W [g] = 面積 S [cm2] × 物体の高さ H [cm] × 物体の密度ρ [g/cm3] よりも 浮力が大きい場合は、物体は浮き 浮力と等しい場合は、物体は静止し 浮力が小さい場合は、物体は沈みます。 |
||||||
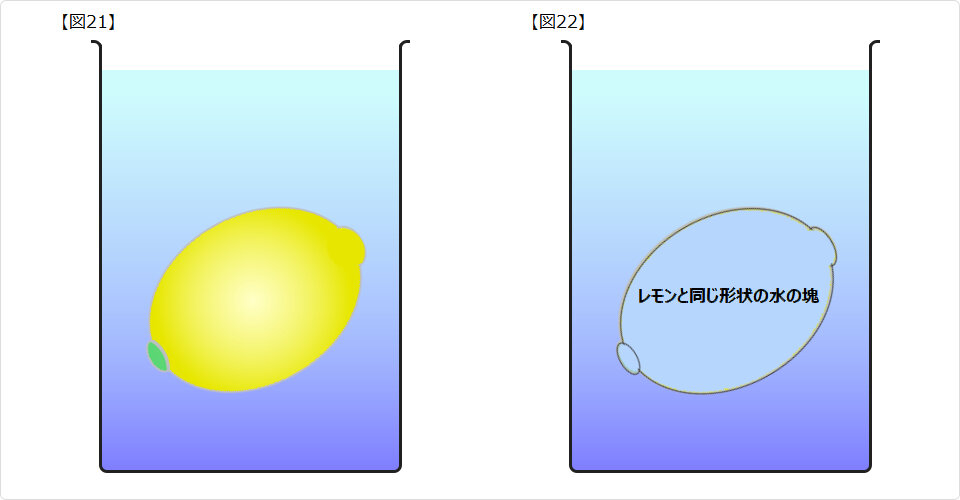
 任意形状の物体に働く浮力 任意形状の物体に働く浮力 |
||||||
 |
||||||
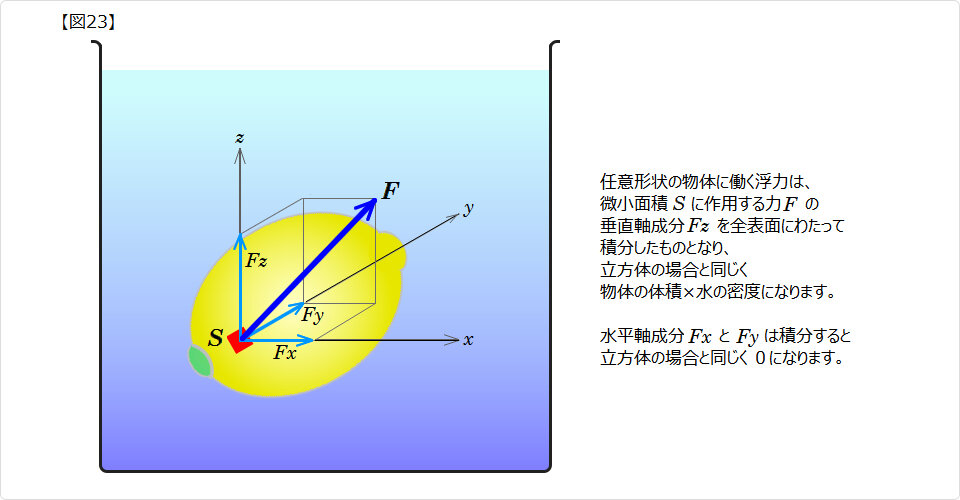
| ▲ 水中に没しているレモンについて考えてみます。 図21 のレモンを 図22 で、レモンと同じ形状をした水の塊に置換えます。 この水の塊は水中で浮きもせず沈みもせずに静止しますから、水の塊の重さ=浮力です。 このことから 浮力は物体の体積で決まり 形状に依存しない ということになります。 ■ よって、浮力は次のようになります。 浮力F [g] = 水の密度ρw [g/cm3] × 物体の水中の体積V [cm3] ■ 浮力を表す誘導式 F = ρV は、原理式で表される多くの重要な要素が欠落しています。原理を理解しましょう。 上式を鵜呑みにすると 水中にある物体には何が何でも浮力が働くという説 に陥り易くなってしまいます。 |
||||||
 任意形状の物体に働く浮力を計算で求めるには 任意形状の物体に働く浮力を計算で求めるには |
||||||
 |
||||||
| ここまでのまとめ。 ★ 浮力は物体の水中の体積の水の重さに等しい ★ 浮力は物体の密度に依存しない ★ 浮力は水深に依存しない ★ 浮力は気圧に依存しない ★ 浮力は物体の形状に依存しない。 |
||||||
 水底にある物体に浮力は働くか? 水底にある物体に浮力は働くか? 硬い容器の場合 |
||||||
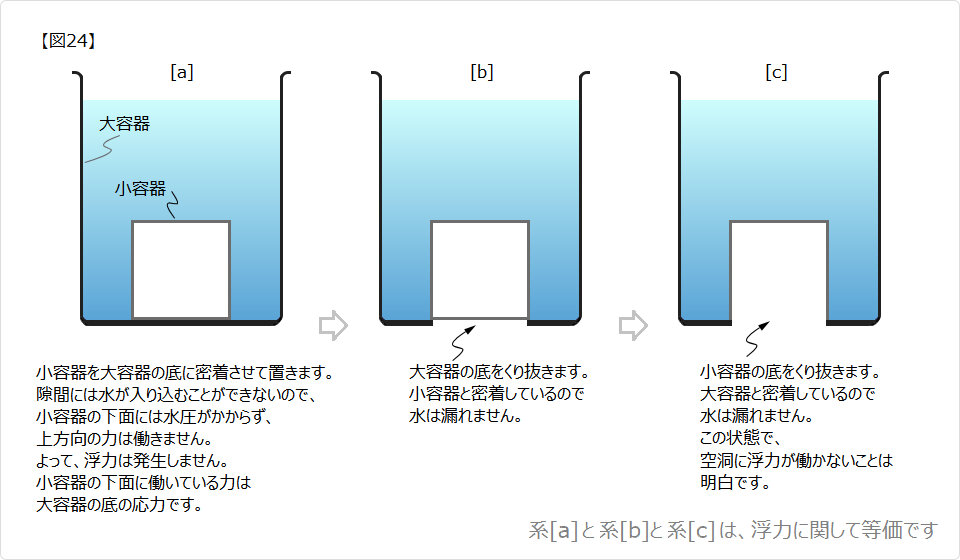 |
||||||
| ▲ 図24[a] において、小容器の下面には水圧がかからないので上向きの力は発生しません。 よって、浮力は発生しません。 ニュートン先生の運動の第二法則 『物体の運動の時間的変化は、力の大きさに比例し、力の方向に作用する』を信じましょう。 ■ 現実では 図24[a] において、どうしても隙間に水が浸み込んでしまうので、浮力が働いてしまいます。 ■ 洗面器を逆さまに風呂の底に押し付けると、しばらくは浮き上がらなくなりますが、 これは吸盤効果によるものです。 |
||||||
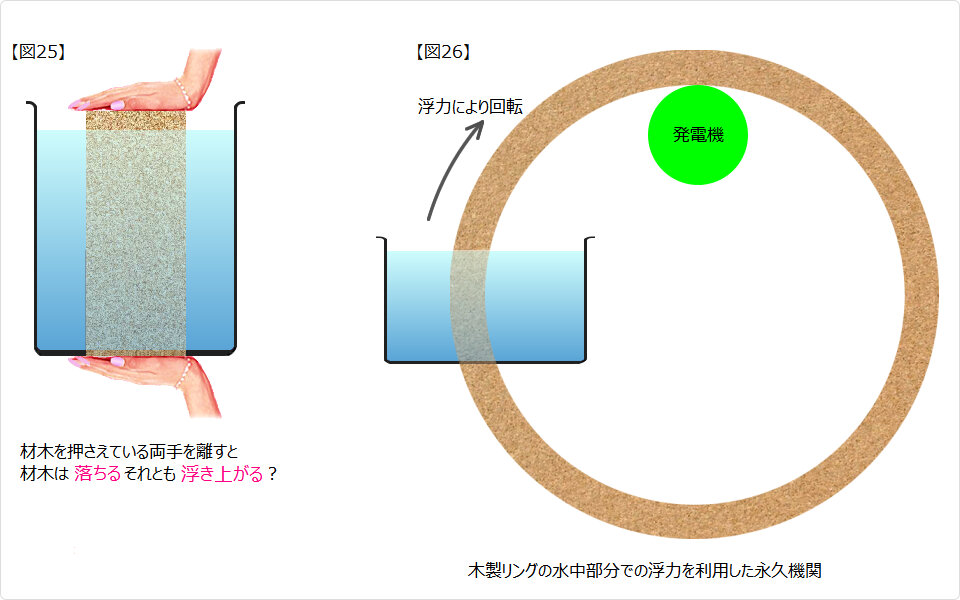 |
||||||
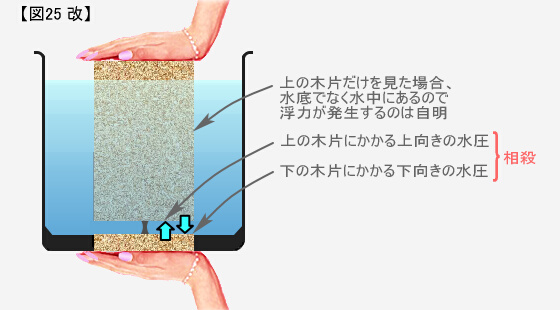
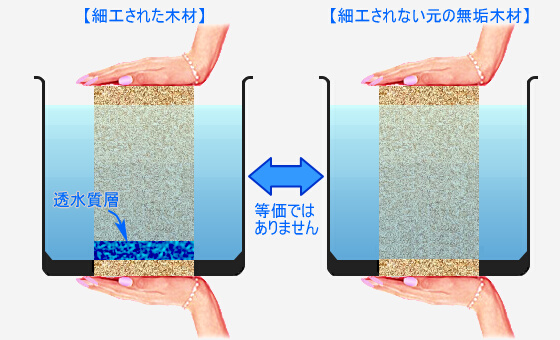
| ▲ 図25 で、両手を離すと材木は落下します。 もし 水中にある物体には何が何でも浮力が働くという説 に従えば、材木は浮き上がります。 すると 図26 の永久機関ができてしまうので、この説は不合理です。 浮力を利用した永久機関は The Museum of Unworkable Devices にたくさん紹介されています。 |
||||||
 水底にある物体に浮力は働くか? 水底にある物体に浮力は働くか? 実 験 |
||||||
 |
||||||
 |
||||||
 |
||||||
 |
||||||
 |
||||||
| ▲ パッキン無しで実験すると、すぐに水が入り込んでしまって失敗。 パッキンを付けても、すぐに水が入り込んでしまって失敗。 パッキンにグリスを塗ると旨い具合に底に沈んだままになりますが、グリスの粘着力が問題。 グリスの粘着力が木製円柱の浮力より圧倒的に小さいことの証明に工夫。 ■ 吸盤効果とか分子間引力で底に張り付いているのではありません。猜疑心が強い方のために補足説明します。  ■ 比重=14の水銀中に比重=8の鉄柱を底にぴったり張り付けると、上と同様に底に張り付いたままになるでしょう。 この場合は、水銀の小さな濡れ性(大きな表面張力)によって鉄柱の底面に水銀が入り込まないので、 ゴムパッキンを付けなくても良いでしょう。 |
||||||
■『水底にある物体に浮力は働かない』という論者
■『水底にある物体に浮力は働く』という論者
■ 着底した潜水艦の浮上問題は、
■「水底にある物体に働く浮力」を求めるペーパーテストにおいて、 出題者は以上のことを良くご理解されていない方が少なくありませんので、完璧な回答を期すためには、 (1)物体が水底に密に接している(物体の底面に水が入り込まない)状態の回答 (2)物体が水底に粗に接している(物体の底面に水が入り込む )状態の回答 を併記するのが宜しいでしょう。 ■ 同様に “ピトー管で速度を測る” というテーマでも、教職に携わっておられる方々で意見が分かれています。 拙筆 “ベルヌーイの定理への素朴な疑問を解決” をどうぞご覧願います。 |
||||||
 水底にある物体に浮力は働くか? 水底にある物体に浮力は働くか? 柔らかい容器(柔らかい物体)の場合 |
||||||
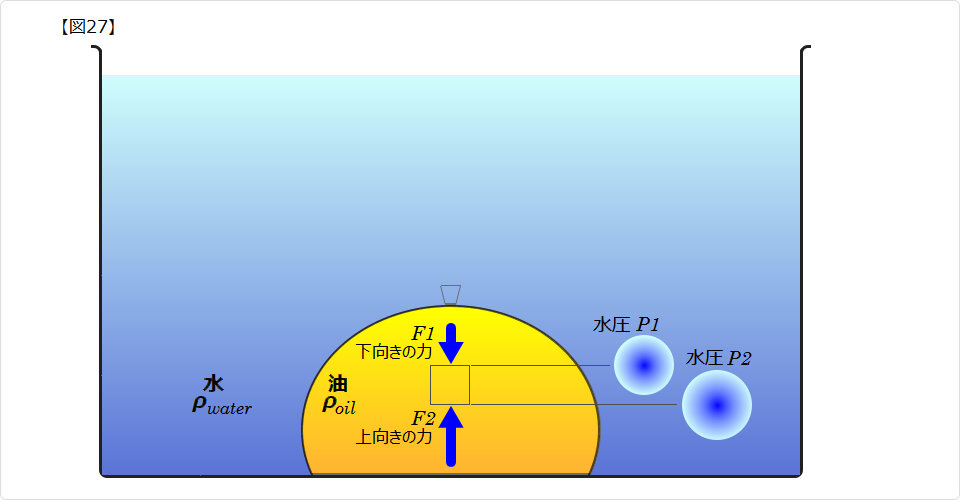 |
||||||
| ▲ 油を入れたビニール袋を底に置いてから、大容器に水を満たすと上図のようになります。 ビニール袋に作用する水圧による力は圧倒的に上面からのもので、下から上向きに働く力は僅かですので、 今までの考え方では、ビニール袋は浮き上がりません。 ■ ところが、水圧は柔らかいビニール袋を通り過ぎて内部の油に伝わります。 この結果、内部の油に不平衡な圧力勾配が生じます。 油の各部が静止する平衡圧力勾配よりも、水の各部が静止する平衡圧力勾配のほうが、傾斜がきつくなります。 ■ 内部の油の直方体の上面に働く力は P1 により、下面に働く力は P2 によります。 直方体の各辺を 1 [cm] とすると、直方体へ働く浮力は F2 − F1 [g] = 面積S [cm2] × 物体の高さH [cm] × 水の密度ρwater [g/cm3] から 浮力 = 1 [g] となります。 一方、油の重さは 体積 1[cm3] × 油の密度 ρoil [g/cm3] = ρoil [g] となります。 浮力 = 1 [g] > ρoil [g] ですので、直方体は浮き上がります。 ■ 即ち、容器(ビニール袋)が持ち上げられるのではなく、油そのものの浮力で浮き上がることになります。 ■ 柔らかい物体内部の圧力勾配を電子計算機でシミュレーションしたグラフを、 IHI 石川島播磨重工業 Top > 技術紹介 > IHI技報 > 第48巻 第4号(平成20年9月発行)-創刊70周年記念号- の、 5.コラム 『お豆腐の話』技術開発本部 小野塚氏 4c873517e9fd9398fdf6ce1f161f8da0.pdf から援用します。 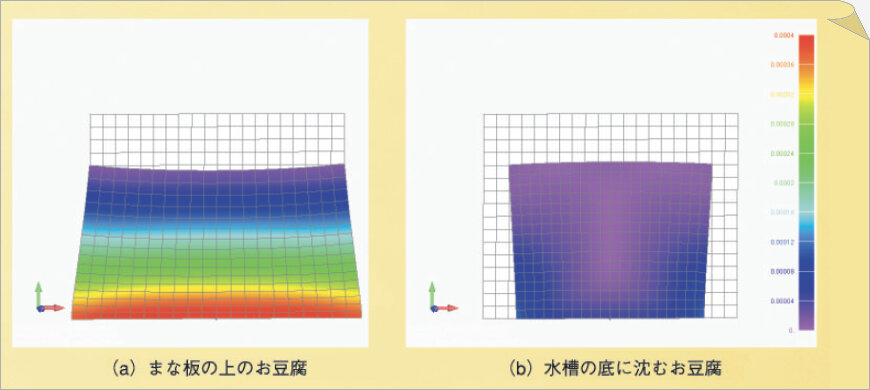 豆腐内部の不平衡圧力勾配により、豆腐自身に浮力が発生します。 ■ ということで、柔らかい容器(柔らかい物体)の場合は下からの力が働かなくても浮き上がります。 ■ これに反して前述したように、硬い容器では内部が液体であっても 内部の液体に不平衡な圧力勾配が生じないので、内部の液体自身の浮力は発生しません。 硬い容器と柔らかい容器(柔らかい物体)を区別して考えることが必要です。 |
||||||
| ここまでのまとめ。 ★ 硬い物体では、 水圧は物体の表面にかかる。 ★ 柔らかい物体では、水圧は物体の内部(物体自身)にかかる。 ★ ニュートン先生の運動の第二法則 『物体の運動の時間的変化は、力の大きさに比例し、力の方向に作用する』を信じましょう。 力が働かなければ物体は動きません。 |
||||||
 離底問題.水底にある物体の重さを測る 離底問題.水底にある物体の重さを測る |
||||||
 |
||||||
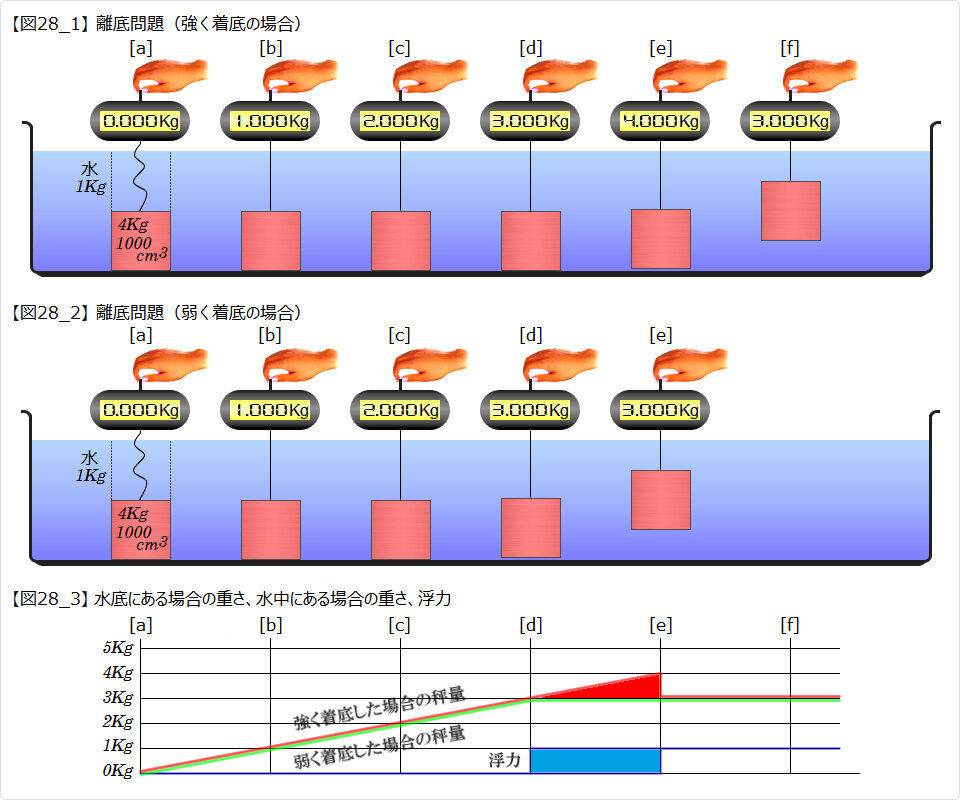
| ▲ 水底に置かれた 4Kg 1000cm3 の金属塊を吊秤で徐々に持ち上げたときのようすを考えてみます。 金属塊の上には 1Kg の水が乗っています。 ■ 図28_1 は、水底に強く着底した場合です。 金属塊の下面に水が入り込めるのは、吊秤が金属塊の重さ 4Kg を 1μg でも上回る力で引っ張り上げた瞬間です。 理屈ではこうなりますが、実際はどうしても水が入り込んでしまうので秤量が 4Kg になることは無いでしょう。 ■ 図28_2 は、水底に弱く着底した場合です。 金属塊の下面に水が入り込める瞬間を下図に記します。この場合は 3Kg になります。 ■ よって、金属塊の着底の強さにしたがって、秤量が 3Kg 〜 4Kg の間のどこかで離底します。 グラフの [d] 〜 [e] の区間です。但し、粘着力とか分子間引力などは無いものとします。 ■ このことから、水底にある物体の重さ(離底する瞬間の重さ)を吊秤で測ると、 着低の強度により 3Kg 〜 4Kg 間のいずれかの重さであると測定されることになります。 着底した物体の重さを吊秤で正確に測定することは原理的に不可能です。 ■ 水底にある物体の離底問題は、 摩擦面に置かれた物体に力を加えた際に、力が最大静止摩擦力に勝って物体が動き出す有り様と似ています。 物体が動き出してしまえば、後は動摩擦力以上の力で動かせます。 わかりやすい高校物理の部屋 3-2-2-2 摩擦力 ページ中段のグラフの一部を援用します。  グラフに“降伏”による不連続点・特異点があっても、何にも問題ありません。 |
||||||
 浮力 雑感 浮力 雑感 |
||||||
 |
||||||
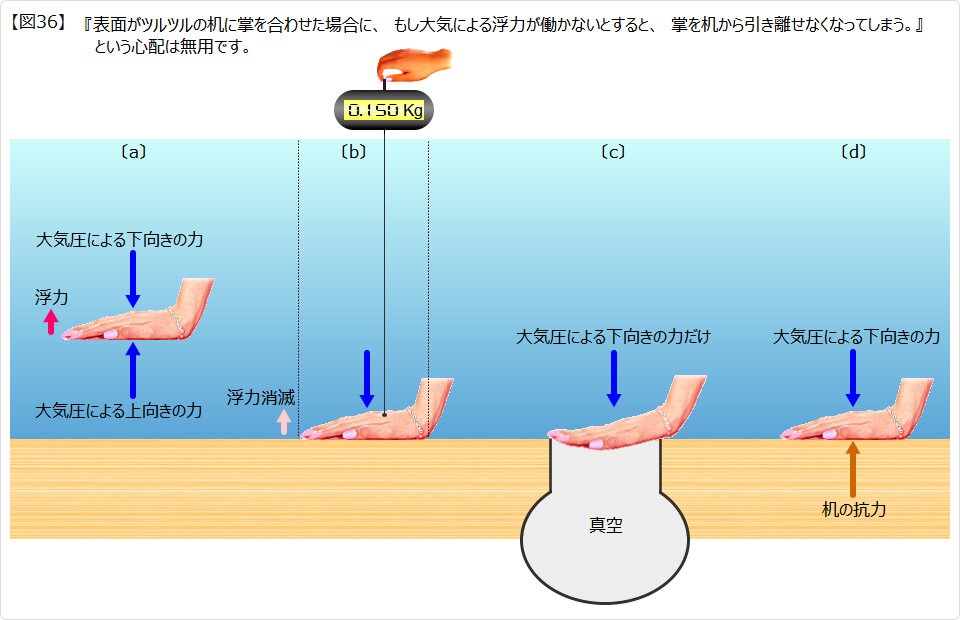
| ▲ 図[a] において、 甲には大気圧による下向きの力が働き、掌には大気圧による上向きの力が働きます。 手が 図[b] のようにツルツルの机に掌を合わせた場合に、“水底にある物体にも浮力は働く”という論者にしてみると、 もし浮力が消滅すると、 論点1:甲にかかる大気圧による下向きの力だけになって、掌を机から離すことができなくなってしまう。 論点2:掌を机から引き離すための必要な力は、 上向きの力が一切働かないので、 手自体の重さに、手の甲に乗っている空気の重さを(水中の場合は水の重さも)加えた重さに等しくなる。 と本気で心配されているようです。 論点1:は 図[c] のようになってしまうと言うことです。これは不合理です。 実際は 図[d] の如く、大気圧による上向きの力の替りに、机の抗力が掌にかかっています。 論点2:手の甲に乗っている空気は(水中の場合は水も)、手の甲による下からの力を受けなくても、 自分自身で浮力を発生します。 ← 図27 柔らかい容器を参照願います 引き離す力は最大でも浮力を受けないときの手の重さになります。 ← 図28 離底問題を参照願います ■ ということで、机に張り付いた掌は浮力が働かなくても容易に引き離すことができます。 地面に張り付いた足も同じです。 ■ 風呂のゴム栓を水抜き穴に差込んだ状態が 図[c] に似て、底にぴったり置いた状態が 図[d] です。 ゴム栓を底にぴったり置いて上向きの浮力が無くなっても、容易に引っ張り上げることができます。 |
||||||
 お疲れ様でした おしまい お疲れ様でした おしまい |
||||||
■  イラストは、商用利用OK、加工編集OK、連絡不要、リンク不要のフリー素材サイト イラストは、商用利用OK、加工編集OK、連絡不要、リンク不要のフリー素材サイトKingyomon Degital Studio (運営者:ヒロシ)様 より拝借しました。星の数ほどある素材サイトの中で秀逸です。感謝。  |